两种常用的相关系数
皮尔逊相关系数和斯皮尔曼相关系数
可以用于衡量两个变量之间相关性的大小

通过抽取的样本的统计量来估计总体的统计量
例如使用样本均值、样板标准差来估计总体的均值（平均水平）和总体的标准差（偏离程度）

一、皮尔逊相关系数

（一）总体皮尔逊相关系数

（二）样本皮尔逊相关系数

（三）皮尔逊相关系数的几个误区

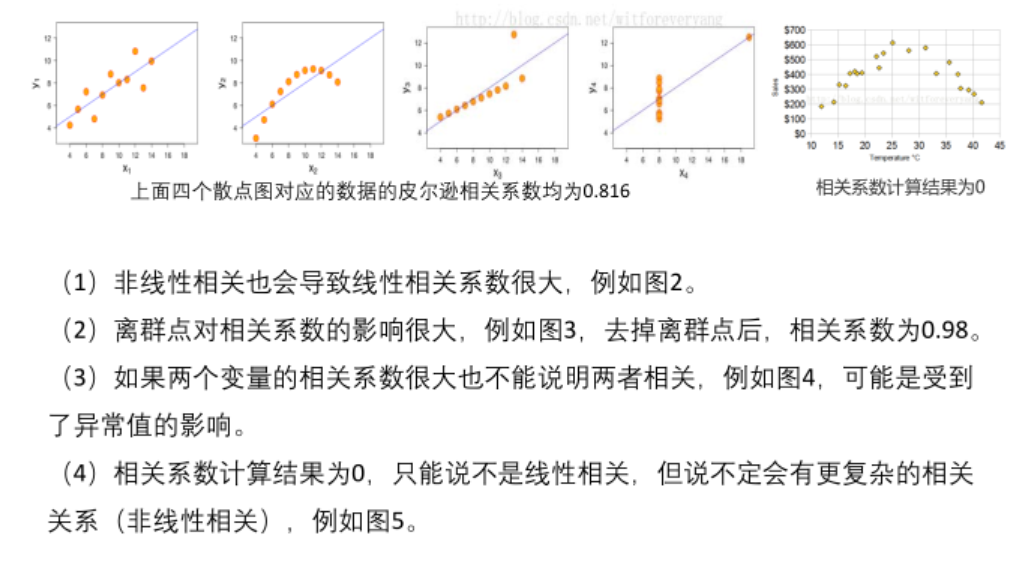
必须要先确认两个变量是线性相关的，然后才能哟管皮尔逊相关系数去了解相关程度。

（四）总结

如果样本室线性的关系，那么皮尔逊相关系数绝对值大的相关性强，小的相关性弱；
在不确定两个变量是什么关系的情况下，即使算出皮尔逊相关系数，发现很大，也不能说明两个变量线性相关，甚至不能说相关，必须先画散点图。

二、假设检验

因为样本只是局部，所以可能存在一些问题，因此事实上，比起相关系数的大小，我们往往更关注的事显著性（假设检验）

（一）过程

1.描述性统计

统计一下基本的特征

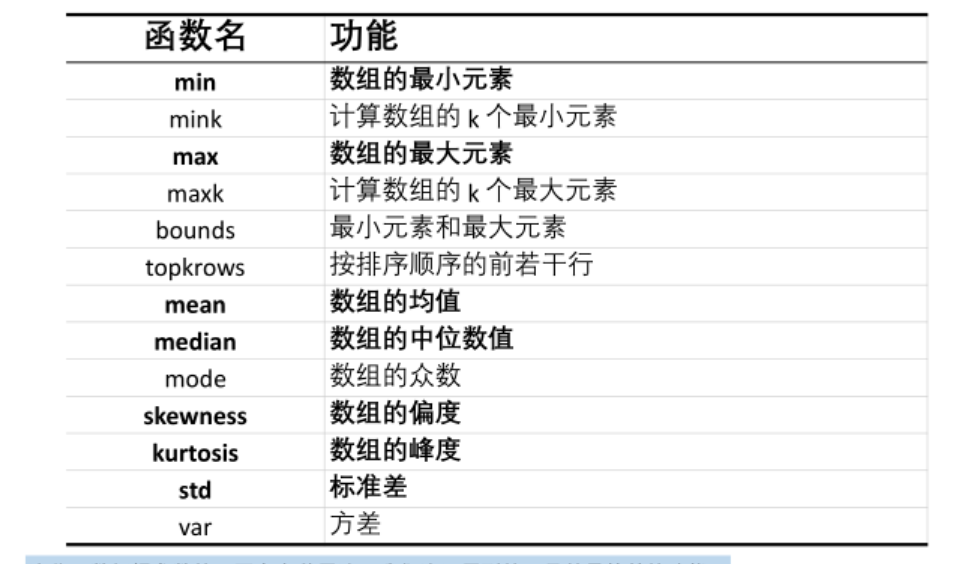
2.绘制散点图

3.皮尔逊相关系数计算

计算之后可以考虑美化可视化展示。

4.对皮尔逊相关系数进行假设检验

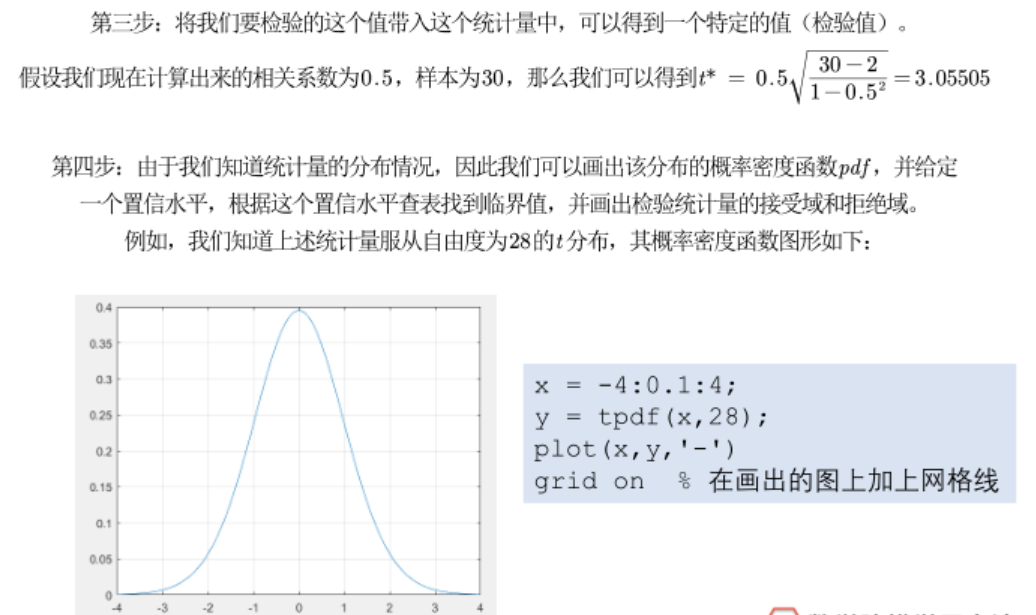
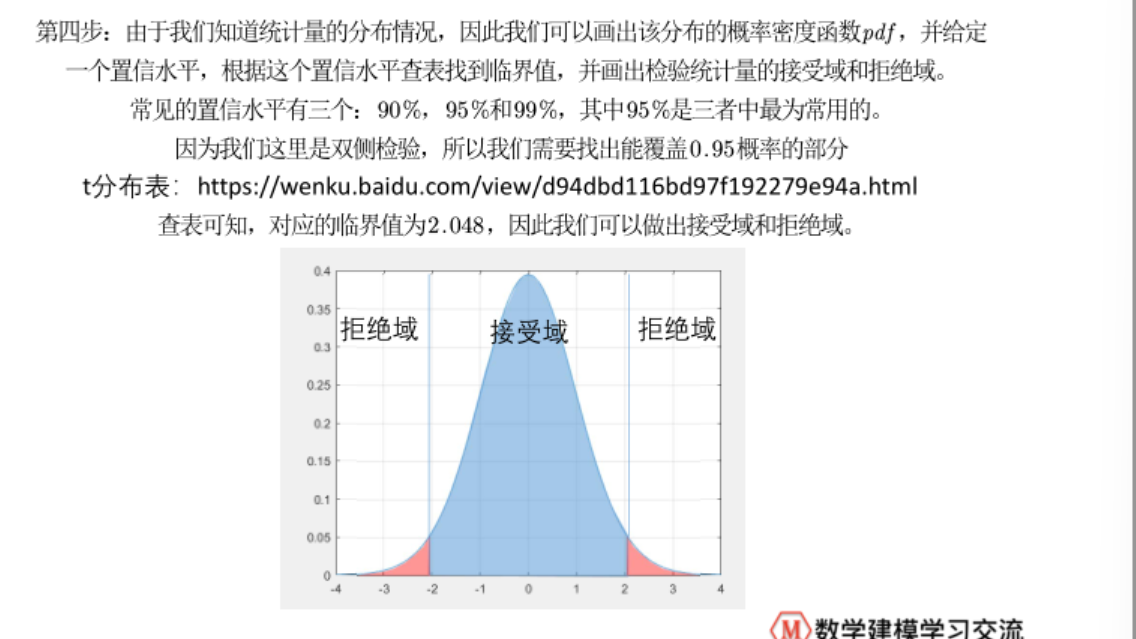
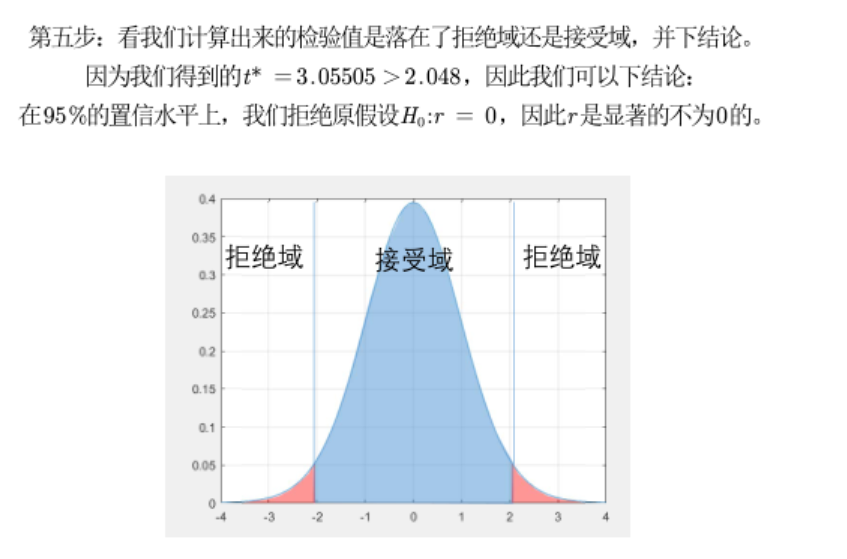
p值判断法

可以考虑直接利用p值判断法确定

（二）条件

皮尔逊相关系数假设检验存在条件
1.实验数据通常假设成对来自正态分布的总体
2.实验数据之间差距不能太大
3.每组样本之间时独立抽样的

（三）如何检验数据是否是正态分布

1.JB检验（大样本n>3）

2.Shapiro-wilk夏皮洛-威尔克检验

3.Q-Q图（不常用，要求n非常大）

三、斯皮尔曼spearman相关系数

（一）定义

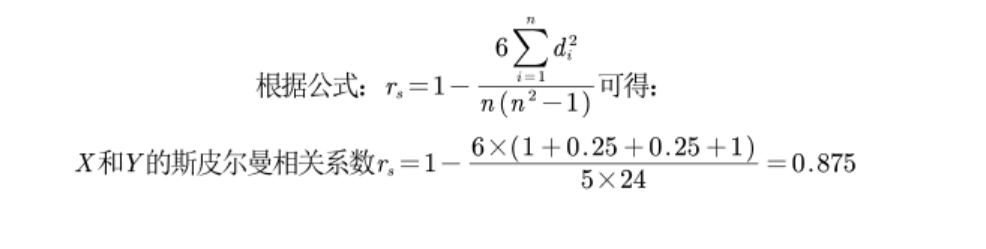
（二）斯皮尔曼相关系数的假设检验

分为大样本与小样本
小样本情况，即n<=30时，直接查临界值表即可。

大样本情况，进行计算

四、两种相关系数比较

1.连续数据，正泰分布，线性关系，用pearson相关系数最恰当，用spearman相关系数也可以，就是效率没有pearson相关系数高。

2.以上任一条件不满足，就用spearman相关系数，不能用pearson相关系数。

3.两个定序数据之间也用spearman相关系数，不能用pearson相关系数。